2024届全国高考分科调研模拟测试卷 老高考(二)数学试卷答案,我们目前收集并整理关于2024届全国高考分科调研模拟测试卷 老高考(二)数学得系列试题及其答案，更多试题答案请关注我们

2024届全国高考分科调研模拟测试卷 老高考(二)数学试卷答案

以下是该试卷的部分内容或者是答案亦或者啥也没有，更多试题答案请关注微信公众号：趣找答案/直接访问www.qzda.com(趣找答案)

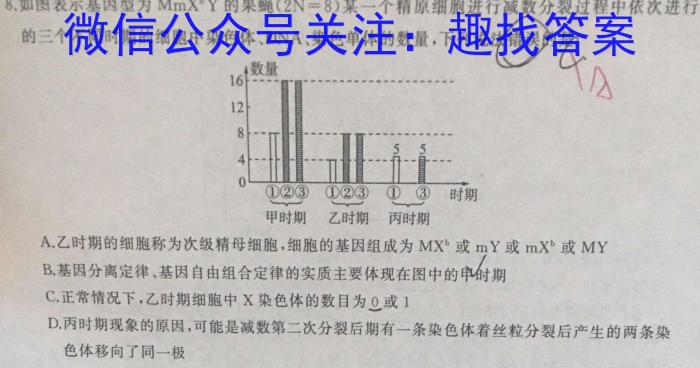
的三个不同时期的细胞中染色体、DNA、染色单体的数量,下列说法错误的是4△A.乙时期的细胞称为次级精母细胞,细胞的基因组成为MX^b或mY或mX^b或MYB.基因分离定律、基因自由组合定律的实质主要体现在图中的申时期C.正常情况下,乙时期细胞中X染色体的数目为0或1D.丙时期现象的原因,可能是减数第二次分裂后期有一条染色体着丝粒分裂后产生的两条染色体移向了同一极

分析由奇函数的性质：f（0）=0，可得n=0，再由g（x）=x+$\frac{m}{x}$在区间$（1，\frac{3}{2}]$上没有最大值．由g（x）在x=$\sqrt{m}$处取得极小值，讨论区间$（1，\frac{3}{2}]$与极值点的关系，即可得到m的范围．

解答解：定义域为R的奇函数f（x），即有f（0）=0，
则n=0，又m＞0，
由f（x）=$\frac{1}{x+\frac{m}{x}}$在区间$（1，\frac{3}{2}]$上没有最小值，
即为g（x）=x+$\frac{m}{x}$在区间$（1，\frac{3}{2}]$上没有最大值．
由g（x）在x=$\sqrt{m}$处取得极小值，
当$\sqrt{m}$≥$\frac{3}{2}$，即m≥$\frac{9}{4}$时，区间$（1，\frac{3}{2}]$为g（x）的减区间，成立；
当1≤$\sqrt{m}$＜$\frac{3}{2}$，且g（1）＞g（$\frac{3}{2}$），即有1≤m＜$\frac{9}{4}$，且m＞$\frac{3}{2}$，
综上可得，m的范围是m＞$\frac{3}{2}$．
故选：D．

点评本题考查函数的性质和运用，主要是奇函数的性质，考查函数的最值的求法，注意运用基本不等式和函数的单调性，属于中档题．