尚文原创 2023届云南名校高考适应性月考试卷(八)数学试卷 答案(更新中)

尚文原创 2023届云南名校高考适应性月考试卷(八)数学试卷答案,我们目前收集并整理关于尚文原创 2023届云南名校高考适应性月考试卷(八)数学得系列试题及其答案，更多试题答案请关注我们

尚文原创 2023届云南名校高考适应性月考试卷(八)数学试卷答案

以下是该试卷的部分内容或者是答案亦或者啥也没有，更多试题答案请关注微信公众号：趣找答案/直接访问www.qzda.com(趣找答案)

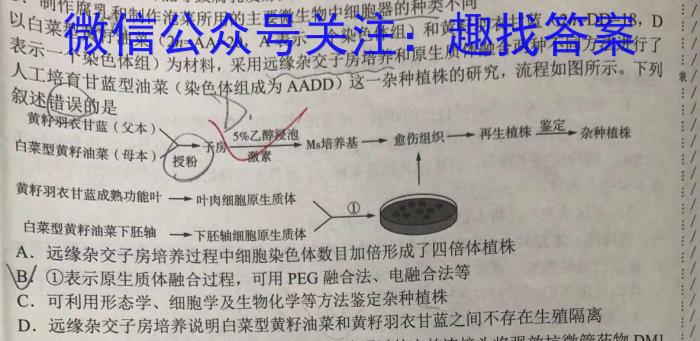
14.以白菜型D、制作腐乳和制作泡菜所用的主要微生物中细胞器的种类不同(2n=AA=20,A表示一个染色体组)为材料,采用远缘杂交子房培养和原生质体融合两种不同方法进行了)为行叙述错误的是人工培育甘蓝型油菜(染色体组成为AADD)这一植株的研究,流程如图所示。下列.AADD)黄籽羽衣甘蓝(父本)(2n=DD=18,D黄籽油菜(2n=AA=20,A表示一个染色体组)和黄籽羽衣甘蓝(2n=DD=18,D白菜型黄籽油菜(母本)5%乙醇浸泡子房Ms愈伤组织一再生植株鉴定,植株授粉激素黄籽羽衣甘蓝成熟功能叶一叶肉细胞原生质体白菜型黄籽油菜下胚轴→下胚轴细胞原生质体A.远缘杂交子房培养过程中细胞染色体数目加倍形成了四倍体植株B.①表示原生质体融合过程,可用PEG融合法、电融合法等C.可利用形态学、细胞学及生物化学等方法鉴定植株D.远缘杂交子房培养说明白菜型黄籽油菜和黄籽羽衣甘蓝之间不存在生殖隔离

分析（1）直线l消去参数t，得直线l的普通方程，圆C化为普通方程，求出圆心C到直线l：x+y-3=0的距离，由此能证明直线l与圆C相交．
（2）圆心坐标，直线l的方程求出AB长，当点P不在直线AB上，则这、A、B构成一个三角形，从而||PA|-|PB||＜|AB|，当点P在直线AB上，||PA|-|PB||≤|AB|，由此能求出||PA|-|PB||的最大值．

解答证明：（1）直线$l：\left\{\begin{array}{l}x=1-\frac{{\sqrt{2}}}{2}t\\y=2+\frac{{\sqrt{2}}}{2}t\end{array}\right.，（t为参数）$中，
消去参数t，得直线l的普通方程为x+y-3=0．
圆$C：\left\{\begin{array}{l}x=1+\sqrt{2}cosθ\\y=1+\sqrt{2}sinθ\end{array}\right.，（θ为参数）$化为普通方程，
得：（x-1）²+（y-1）²=2，圆心C（1，1），半径r=$\sqrt{2}$，
圆心C（1，1）到直线l：x+y-3=0的距离：d=$\frac{|1+1-3|}{\sqrt{1+1}}$=$\frac{\sqrt{2}}{2}$$＜r=\sqrt{2}$，
∴直线l与圆C相交．
解：（2）过圆心C作CD⊥AB，交AB于D，由（2）得CD=d=$\frac{\sqrt{2}}{2}$，
∴AB=2AD=2$\sqrt{{r}^{2}-C{D}^{2}}$=2$\sqrt{2-\frac{1}{2}}$=2×$\frac{\sqrt{6}}{2}$=$\sqrt{6}$．
当点P不在直线AB上，则这、A、B构成一个三角形，∴||PA|-|PB||＜|AB|，
当点P在直线AB上，||PA|-|PB||≤|AB|=$\sqrt{6}$，
∴||PA|-|PB||的最大值为$\sqrt{6}$．

点评本题考查直线与圆相交的证明，考查两线段之差的绝对值的最小值的求法，是中档题，解题时要认真审题，注意点到直线的距离公式的合理运用．

尚文原创 2023届云南名校高考适应性月考试卷(八)数学